Project 2: Filters and Frequencies
1.1 Finite Difference Operator

To produce an edge image of "Cameraman.png," we use the finite difference operators Dx = np.array([[1, -1], [0, 0]]) and Dy = np.array([[1, 0], [-1, 0]]). By convolving the cameraman image with each of these operators, we can visualize the partial derivative of both Dx and Dy. We can combine these to produce a gradient magnitude image and then binarize to get our final edge image.




1.2 Derivative of Gaussian


To better improve our results and minimize noise, we can use a Gaussian filter to blur our image first, then again perform the same Dx and Dy convolutions on our image to produce a more defined edge image. Compared to the finite difference operator, our gradients are more defined.


.jpg)
.jpg)
Interestingly enough, this produces the same result even if we were to change up the order. If we instead convolve the Gaussian with each of Dx and Dy first, and then compute the gradient magnitude binarized image, we will have the same result as when we convolved the Gaussian with the image first and then computed the gradient magnitude binarized image using Dx and Dy.


.jpg)
.jpg)
As you can see below, the two results are essentially identical.
.jpg)
.jpg)
2.1 Image Sharpening
To sharpen an image, I used high pass filtering by defining my own unsharp mask filter. This is done by subtracting the original image by its blurred version (convolved with 2D Gaussian), which will result in the high frequencies of the image. Then, I can multiply this difference by an alpha factor to change the intensity of sharpness--here I used alpha = 2. Finally, I can combine these (magnified) high frequencies with the original image to get a sharpened image.






This technique can be employed with an already sharpened image, too. I first blur my sharp image and then sharpen it again, and the results seems to be pretty similar. There is some information that is lost from the initial blurring, however, which is why the sharpened image is similar but not quite the same as the original.




2.2 Hybrid Images
To produce a hybrid image, both images are first aligned. Then, Derek is blurred using a Gaussian filter whereas Nutmeg is sharpened using a unsharp mask filter, and the two are laid on top of each other. For the color image, I processed each channel individually and combined them correspondingly.






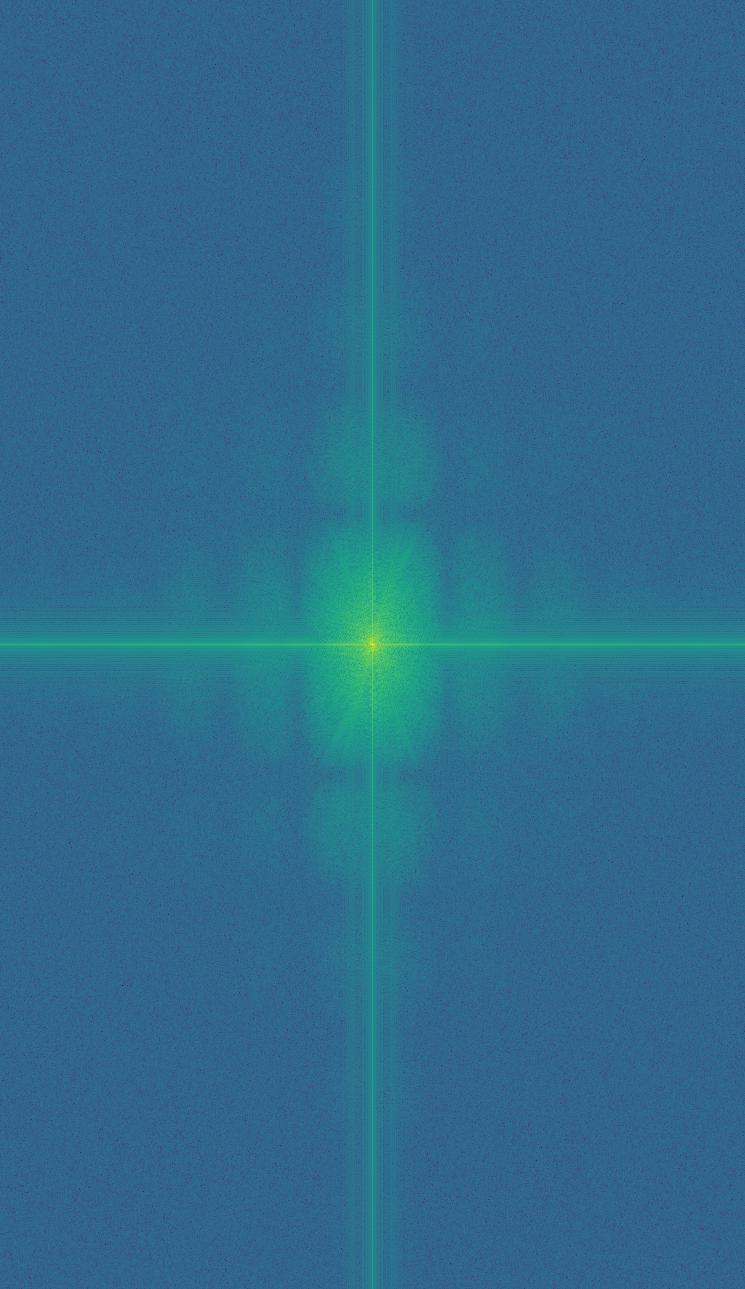
These are the FFTs of the images. After Derek is blurred with a Gaussian filter, this results in the blocky pattern as seen in the FFT as well as higher alignment along the vertical and horizontal lines, indicating lower frequencies. Sharpening nutmeg increases the proportion of higher frequencies, hence causing a larger blur/range of lighter values. Therefore, the hybrid is brighter/higher frequency than the blurred image but darker/lower frequency than the sharpened image.










2.3 Gaussian and Laplacian Stacks